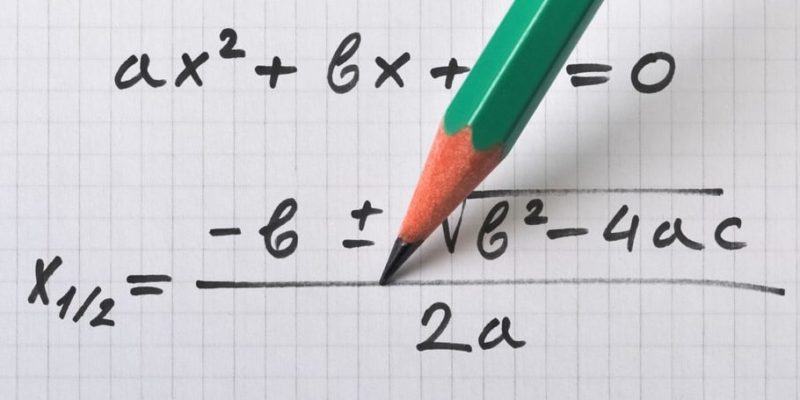ÁLGEBRA 

¿Qué es la Álgebra?

El estudio de la matemática comienza con los números; primero los números naturales y los enteros y sus operaciones aritméticas, que se clasificarían dentro del álgebra elemental. Las características más avanzadas sobre números enteros se estudian dentro de la teoría de números.

 A continuación, encontraras un video explicando algunos términos del algebra para que entremos más en contexto.

Historia del Álgebra: 

El álgebra nació en la cultura árabe, alrededor del año 820 d. C., fecha en que se publicó el primer tratado al respecto: Al-kitāb al-mukhtaṣar fī ḥisāb al-ŷarabi waˀl-muqābala, es decir, “Compendio de cálculo por reintegración y comparación”, obra del matemático y astrónomo persa Muhammad ibn Musa al-Jwarizmi, conocido como Al Juarismi.

 ¿Para qué sirve la Álgebra?

Al Juarismi creó el álgebra en el siglo IX.

Permite llevar a cabo presupuestos, facturación, cálculos de costos, beneficios y ganancias.

Además, otras operaciones de importancia en la contabilidad, administración e incluso la ingeniería, se sostienen en base a cálculos algebraicos que manejan una o varias variables, expresándolas en relaciones lógicas y patrones detectables.

Ramas de la Álgebra: 

Álgebra elemental. Como su nombre lo indica, comprende los preceptos más básicos de la materia. Esto es, fundamentalmente, el manejo de ecuaciones y de variables, incógnitas, coeficientes, índices o raíces.

Álgebra abstracta. Representa un grado mayor de complejidad respecto a la elemental, ya que se dedica al estudio de las estructuras algebraicas o sistemas algebraicos, que son conjuntos de operaciones asociables a elementos de un grupo de patrón reconocible.

Expresiones algebraicas: 

En ellas reconoceremos números y letras (variables), pero también otro tipo de signos, y de disposiciones, como los coeficientes (números antes de una variable), grados (superíndices) y los signos aritméticos usuales. En líneas generales, las expresiones algebraicas pueden clasificarse en dos

• Monomios. Una expresión algebraica sola, que posee en sí misma toda la información que se requiere para resolverla. Por ejemplo: 6X2 + 32y4

• Polinomios. Cadenas de expresiones algebraicas, o sea, cadenas de monomios, que poseen un sentido global y deben resolverse en conjunto. Por ejemplo: 3n5y3+23n5y8z3 – π2 3n – 22 + 26n4.